于计算机科学领域内,若我们去探究一个数字的所谓“源码”,通常所指的乃是其于二进制世界里的初始呈现模样。就数字十三而言,它的源码、反码以及补码在计算机内部的呈现情形,是搞清楚计算机数据存储与运算基础的关键要点。这些二进制编码不但构成计算机科学的基础,还直接对硬件如何处理整数运算施加影响。无论是简单的算术运算还是复杂的系统操作,都必须建立在对这些基本表示方式的掌握之上。
13的源码怎么表示
于二进制体系内,数字13的源码展现得相对径直,13的源码就是其径直的二进制样子,借由除2取余这种运算办法,十进制数13变成二进制是1101,在计算机当中,我们一般运用固定位数来表示整数例如8位,于是,在8位二进制表示里,13的源码便是,在此要特别留意,源码的最高位是符号位,这个符号位中0代表正数,1代表负数。鉴于13属于正数,所以其符号位为0,数值的部分是1101,合并起来成为 ,关于正数而言,它的源码以及反码和补码是三码合一的,这表明,13的反码以及补码同样是 。
负数的反码如何计算
完成对正数表示的领会活动之后,负数的编码形式展现出明显不同。负数做反码计算有特定准则:先得到该负数的源码,然后维持符号位不变,将数值部分的每个二进制数位进行取反操作,即把0变为1,把1变为0。以-13为例,它的源码是表示负数的最高位数字为1的 。于开展反码计算之际,我们使符号位那个“1”持续保持不变状态, 针对数值那部分的“”予以取反的这类操作, 进而得到“”这个结果, 所以说“-13”的反码便是“” 。 此等进行取反这项操作, 可不只是计算机当中的一种数学运算方式, 还是在硬件层面之中, 依靠简单的逻辑门电路从而就能高效实现的一个过程, 它彰显出了计算机设计所拥有的巧妙之处 。
补码在计算中有什么优势
现如今,于现代计算机系统之中占据主导地位的是补码表示法,这事主要是因为它具备几个关键的优势哦。其中之一呢,补码将零的表示给统一了起来,在补码的系统情境里头,零仅仅存在全零这样一种表示形式,成功地把源码以及反码当中所存在的“正零”与“负零”问题给巧妙地避开了哟。其二呀,补码使得计算机的硬件设计得以简化,加、减法之类的运算能够借助同一套电路去达成,这是因为减去一个数意味着加上该数的补码呢。比如说呀,在进行9 – 6的计算之时,计算机实际上执行的便是9 + (-6的补码)这样的运算,最终顺利得出正确的结果3啦。这样的设计,将CPU的复杂度大幅降低了,并且把运算效率提高了,而且,补码表示使得溢出检测变得更为直接且统一了。
进制转换如何实际操作
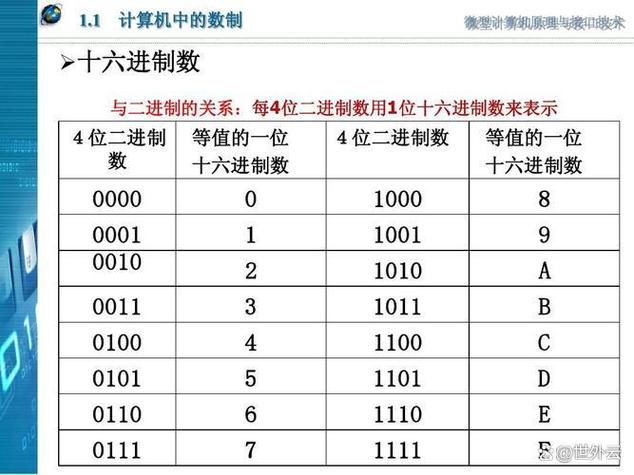
了解不同进制相互之间的转换办法,对于明白计算机当中的数据呈现来讲极为重要。将十进制转换为二进制,最为常用的方法是“除2取余法”:不断用2去除十进制数,并记录每次的余数,直到商为0,然后将余数倒序排列。例如,把33转换为二进制,通过不断除以2得到余数序列,最终的结果是 。从二进制转换为十进制则采用加权求和的方法,把每一位的值乘2的相应次幂后相加。就二进制与十六进制的转换来讲,由于16是2的4次幕,故而每4位二进制数会对应1位十六进制数。这种进制间的自由转换能力,是深入理解计算机底层机制所必需的技能。
实际编程时,你有没有遇到过,因为对数据底层表示缺乏了解,从而导致的有趣的程序错误,或者面临的挑战呢? 欢迎在评论区分享你的经历,要是觉得本文对你有所帮助,也请点赞,并且分享给更多的朋友。